Applying a Triplet Arpeggio Sequence to the Cycle of Fourths

Last month, we explored playing ascending and descending arpeggios over a cycle-of-fourths chord progression, which is a sequence of chords wherein each is the intervallic distance of a perfect fourth above (or a fifth below) the previous one. To review, the figures in the previous column began on Am; if we count four scale degrees or note letter names up from A — A B C D — we find that D is the intervallic distance of a fourth above A. To find the fourth above D, we apply the same letter counting method — D E F G. So G is the fourth of D. Starting from G, we’d have G A B C, and so on. (Bear in mind, however, that this method can get a little more complex and specific when sharps and flats are involved, but this is basically how it works.) So, our resultant cycle-of-fourths chord progression is either A D G C or, in our application, Am Dm G C. If one were to continue the process through all 12 tones, we can generate the progression Am Dm G C F Bb Eb Ab Db Gb B E, which we can then resolve to A (or Am). In this lesson, I’d like to continue working with this progression and show you how to apply an interesting and useful melodic pattern to it.

FIGURE 1 illustrates the aforementioned chord progression, which, by the way, is not diatonic to, or within the scale structure of, any particular key. Rather, it simply moves through all 12 tones in ascending fourths (or descending fifths). FIGURE 2 presents the arpeggios Am (A C E) and Dm (D F A) played up and down across all six strings through two octaves in fifth position. A common melodic phrasing device in baroque classical music, one that is still widely used today in blues, rock and jazz, is an arpeggio-based note pattern that has you alternately ascending and descending (meaning changing direction with each note) in a rhythm of eighth-note triplets, progressing through every possible neighboring three-note group. FIGURE 3 illustrates this phrasing device applied to our Am arpeggio. Play through the sequence slowly at first, striving for clean articulation of each note.

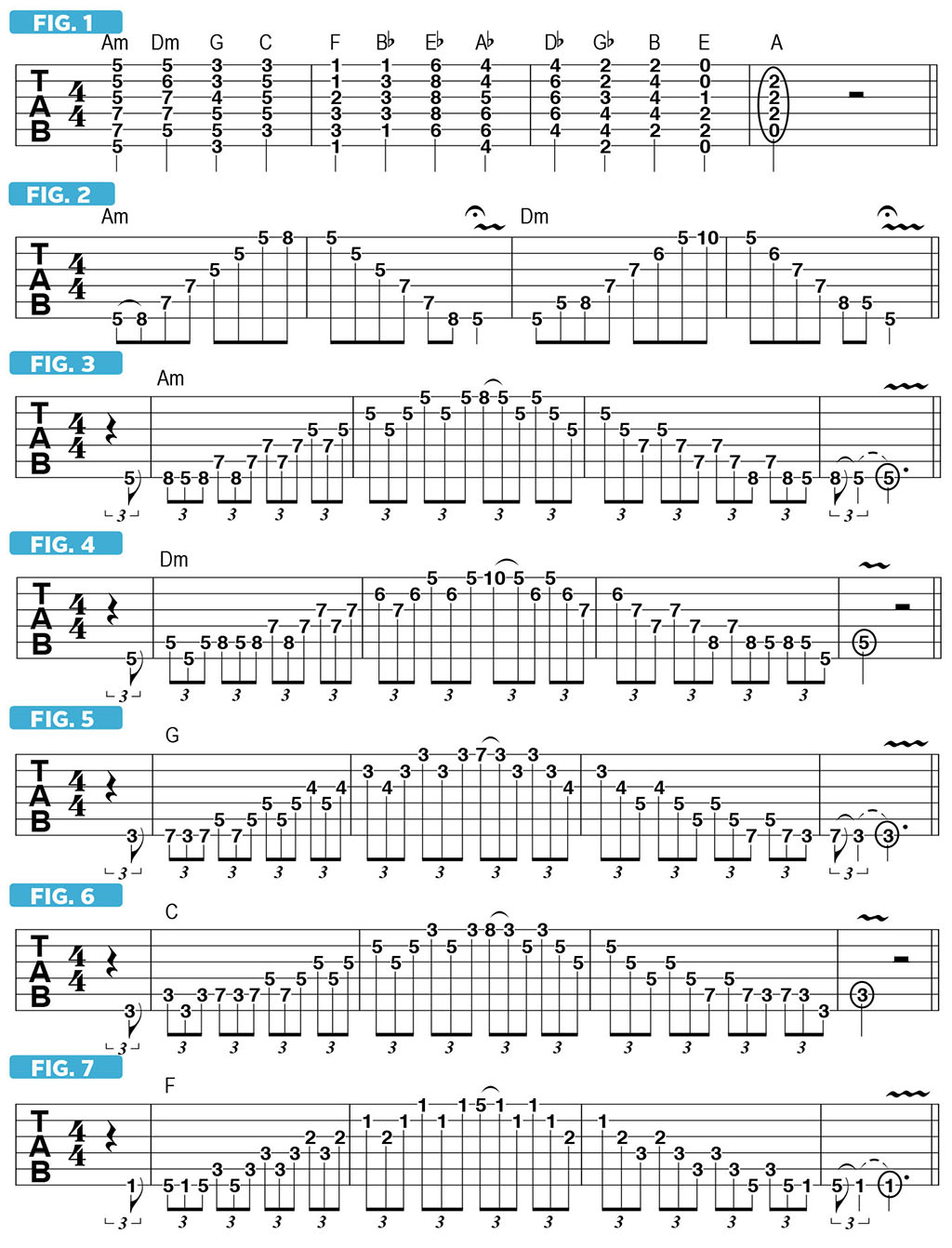
FIGURE 4 applies this same approach to our Dm arpeggio, beginning on the low A note on the sixth string’s fifth fret. Notice that there’s a wide, five-fret stretch in bar 2, with the pull-off from D to A on the high E string. Position your fret-hand thumb squarely on the back of the neck and rotate your wrist as needed, in order to reach the five-fret span.

FIGURES 5-7 continue the triplet-phrasing sequence with the arpeggios G, C and F. As you descend the fretboard, the fret-hand stretches become wider and a little more challenging, so be sure to ease into them and try to keep your fret hand as relaxed an limber as possible. Again, ensure you rotate your wrist as needed to maximize the reach among the fingers.

Guitar World Associate Editor Andy Aledort is recognized worldwide for his vast contributions to guitar instruction, via his many best-selling instructional DVDs, transcription books and online lessons. Contact Andy at andyaledort.com.