What You Need to Know About Intervals

Music was my refuge. I could crawl into the space between the notes and curl my back to loneliness. — Maya Angelou
Intervals are simple, useful and helpful bits of knowledge. They’re a priceless musical commodity, being one of the most fundamental and applicable building blocks of scales and lead sequences. Yet, despite the simplicity, the related theory can get fairly involved. In fact, much of it is outside the scope my own guitar playing. Therefore, I don't need to know it all.
So this guitar interval lesson is limited to information I’ve found to be the most useful and relevant to my instrument of choice. In other words, it’s just what you need to know and nothing more. Note that this is an abridged version of a larger lesson. You can check out the full article on Guitar Chalk and download the PDF lesson outline.
Definition: What Is an Interval? In music theory, an interval is the space between any two pitches (according to Harmony: Its Theory and Practice by Ebenezer Prout). On guitar, it's simply space between any two notes on the fretboard.

Take for example, the following tabbed interval:
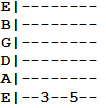
Both notes are separated by two semitones (also called a “half step” or one-fret jump), which are equal to a whole tone or “whole step.” But what if the two notes don’t occur on the same string? Consider the following:
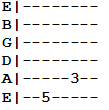
How does this work? Even on different strings there's still a linear line of frets separating any two notes. We still count it the same way. More on this later.
All the latest guitar news, interviews, lessons, reviews, deals and more, direct to your inbox!
What Are the Parts of an Interval?
An interval on the guitar is only two parts: 1. The Root Note 2. The Interval(s) Intervals are always understood in relation to some root note. For instance, the open G in a C chord is not the interval of the note that falls on the second or first fret in the same chord. Rather it’s the interval of the C that falls on the fifth string at the third fret. Why? Because that C note is the chord’s root.
A Guitar Interval Chart
There are a total of 11 different intervals before you get to your first octave, which doubles the frequency of the original note. Therefore each interval should have a “Number of Frets” and an “Interval Quality.” You’ll identify intervals by associating the number of frets with the corresponding interval quality and vice-versa. Here’s a chart displaying this information for all 12 intervals:

So how do we read this chart and translate it to the fretboard? Let’s start with something simple.
Simple Example
You’re in music class and the teacher wants you to draw minor second interval in guitar tab form. What do you do? First, recall from our chart that a minor second is a one semitone interval. That means you’ll have a note that falls one semitone from its root. Since you can choose the root, you’ve got plenty of options. Here’s one:
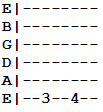
The root note is at the third fret (G) while the interval falls on the fourth fret.
What About a Major Second?
To create a major second, we refer back to our chart, again, which tells us there are two semitones separating our interval and root note. You're probably beginning to see a pattern. Behold, our major second:
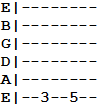
You can continue through the chart in a similar manner.
The Major Third: Notes on Two Different Strings
What’s happening when we have intervals with notes on two different strings? We mentioned earlier that the same principles apply. Using the major third interval as an example, let's draw one up on a tab sheet with the two notes on separate strings.
What do we do first?
Per the chart, there are four semitones separating the interval from the root note in a major third. So this tab would qualify:

However, it’s problematic. The jump from the third to the seventh fret is doable, but lengthy and inefficient. There's a better way to play it. Per the fretboard notes, we know the note at the seventh fret is a B. To get a more optimal interval, simply find another B note on the fifth string that's closer to our root.
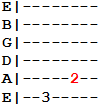
The note we’re looking for is at the second fret (in red). Any B note on any other string will qualify as a major third interval of the root G. For example, the following note is also a B:

Despite being an octave higher, the interval property doesn’t change.
What About the Perfect Fifth?
“Perfect fifth” might be a familiar term to you. If so, that’s good news since it’s one of the most important intervals you can learn. Think two-note power chord:
Power Arpeggio Form

Power Chord Form
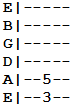
We have our interval note (D) seven semitones above the root (G). The seven-semitone spread gives us the perfect fifth.
Done
This might seem like a lot to digest for such a simple topic. But keep mind, it's not even close to a comprehensive look at intervals, in a music theory sense. It's just enough for us guitar players to be dangerous. So best of luck to you and be sure to keep learning.
Follow Up
You can print this lesson out or download the Guitar Intervals PDF Outline for teaching it yourself or quick review. Questions or thoughts? Shoot me an email bobby@guitarchalk.com. You also can get in touch with us over at Facebook and Twitter.
Robert Kittleberger is the founder and editor of Guitar Chalk and Guitar Bargain. You can get in touch with him here, or via Twitter, Facebook and Google Plus.
Bobby is the founder of Guitar Chalk, and responsible for developing most of its content. He has worked with leading guitar industry companies including Sweetwater, Ultimate Guitar, Seymour Duncan, PRS, and many others.

