If you can hear what’s going on in these patterns and replicate it in other musical situations, then you’ve built a crucial foundational tool for improvising.
(Image credit: Cindy Moorhead)
For those who might not be familiar with intervals, we’ll start by reviewing the core concept.
The term sounds kind of advanced, but an “interval” simply refers to the distance between two notes, while a harmonic interval is when you play two notes at the same time.
So to bring the simplicity home, a power chord is a harmonic interval, and most of us are pretty comfortable with power chords.
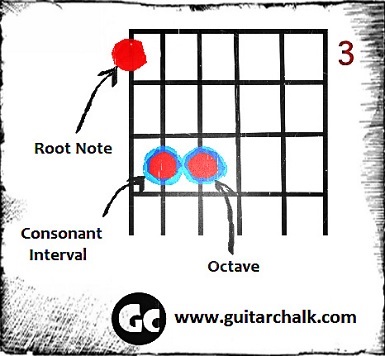
So when you’re playing a “perfect 5th power chord,” you’ll typically have two major components:
01. The root note (typically the lowest note)
02. The consonant interval.
For a power chord that has a root note on the sixth string, you can make it a perfect fifth by simply playing the fifth string two frets up. For example, a G5 power chord would look like this:
If you’ve been playing guitar (particularly electric guitar) for any length of time, you’ll know this chord is incredibly common and is even exclusively used in many songs.
So why does this matter?
Perfect fifths make it incredibly easy to find the consonant interval, which can be simply thought of as two notes that resolve or “sound good together” and don’t leave you wanting. The term “staple” is also used to describe a consonant chord or interval.
Additionally, perfect fifths make it easy for you to find octaves, assuming you’re playing your chord on either the fifth or sixth string.
Playing a power chord on the fourth or third string changes things a bit because of the tuning of the second string to B, which means you have to reach further for one of your consonant notes; three frets up instead of two. This is just something to keep in mind.
For this lesson, we’re just dealing with power chords played on the sixth and fifth strings.
So let’s recap — perfect fifth power chords give us easy access to:
01. A consonant note in an interval 02. The octave of our root note.
Improvisation
It pays to understand this concept whenever you want to start figuring out how to improvise because it gives you a starting point and provides some simple structural components to start out with.
You know now that any power chord with a root note on the sixth or fifth string will have a workable or “stable” note two frets and one string up. Additionally, you’ll have an octave of that note two frets and two strings up.
So, going with the G5 power chord:
Root Note on the Sixth String and Third Fret
• Consonant Note: 5th String and Fifth Fret • Octave Note: 4th String and Fifth Fret
This gives you a bit of a skeleton to build your improvising off of, so the best way to get that anchored in your mind is to go through a few basic exercises that utilize the perfect fifth at several different spots on the fretboard:
Exercise 1: Perfect Fifths Power Chords (Sixth String Root)
Exercise 2: Dyad Chords (Fifth String)
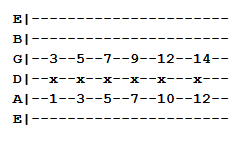
Exercise 3: Perfect Fifths Power Chords (Fifth String Root)
Exercise 4: Combination
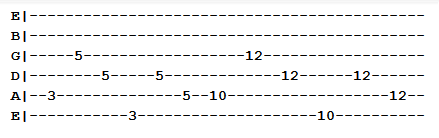
Exercise 5: Combination
Hearing the Consonant Notes and Octaves
Once you understand the concept, the challenge is to start to be able to hear the consonant and octave notes that correspond to your root note. As you develop familiarity with that system, your instincts as a guitar player will start to improve, and your ear will be able to pick up on more subtleties of the instrument.
You’ll know what a consonant and octave note sound like, even if you might not be thinking in those terms as it’s happening.
So in a sense, it’s really more about your ear than it is about what you see on a piece of paper. If you can hear what’s going on in these patterns and replicate it in other musical situations, then you’ve built a crucial foundational tool to help you become better at improvising and playing by ear.
Bobby is the founder of Guitar Chalk, and responsible for developing most of its content. He has worked with leading guitar industry companies including Sweetwater, Ultimate Guitar, Seymour Duncan, PRS, and many others.
